
小6 算数 小6 40 並べ方 組み合わせ方 Youtube
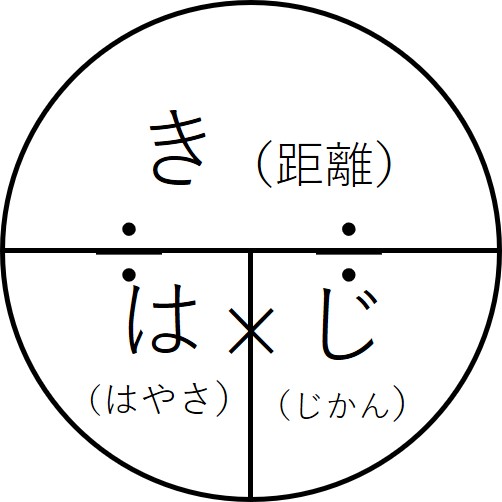
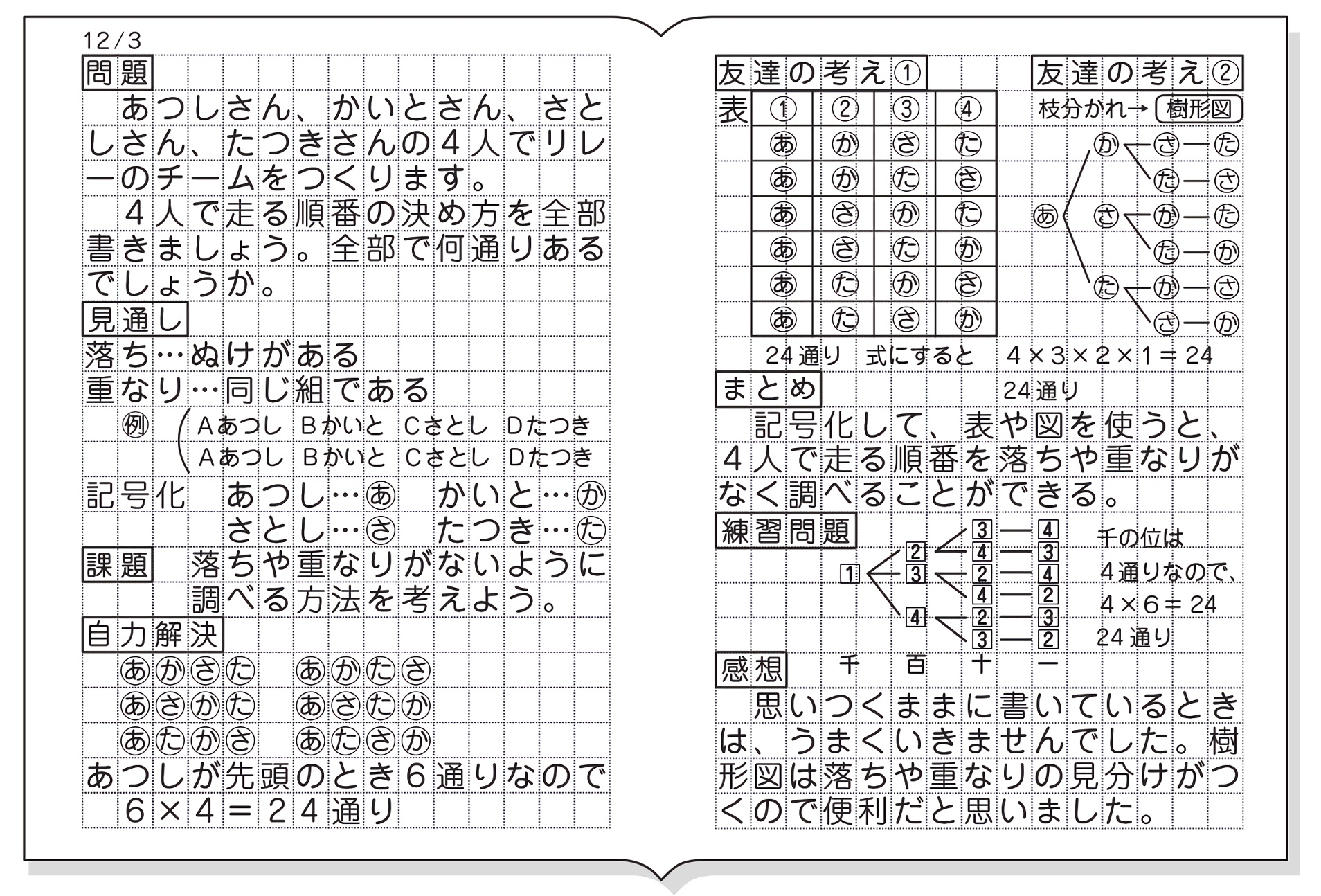
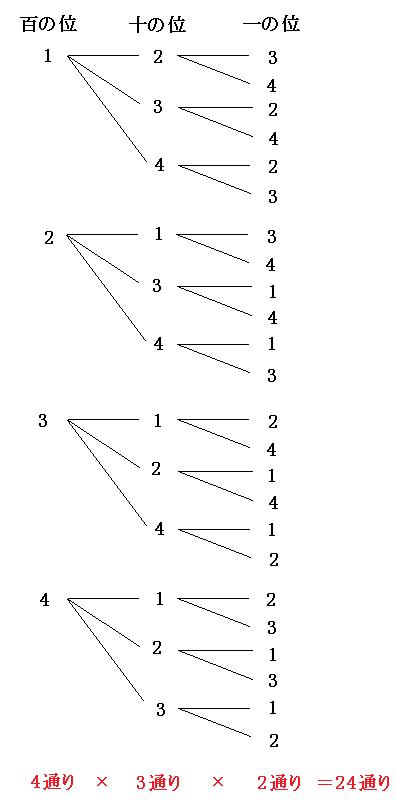
5.ある数は、ある数の何割増なのか? たとえば「今年の売上は100円であり、前年の50円と比べてx割増えた」という計算。 このような『ある数は、ある数の何割増なのか?』という計算は、 「ある数(比べる数)」÷「ある数(比べられる数)」× 10 1、2、3、4のカードを使ってつくれる3けたの整数は何通りありますか。 解法 1から始まるものを必ず順番に書く 123 124 132 134 142 143 他のカードが先頭の時にも6通りずつあるので6×4=24通り 計算のみ解法 100の位が4通り 10の位がそのそれぞれに対して3通り
何通りあるか 計算 小学生
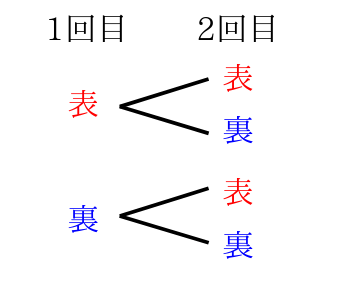
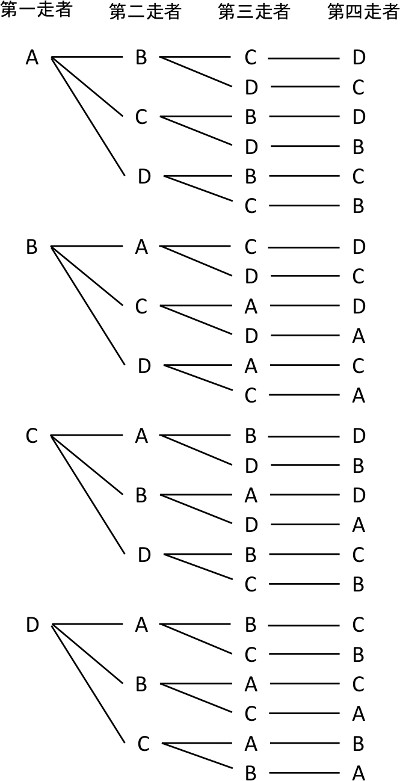
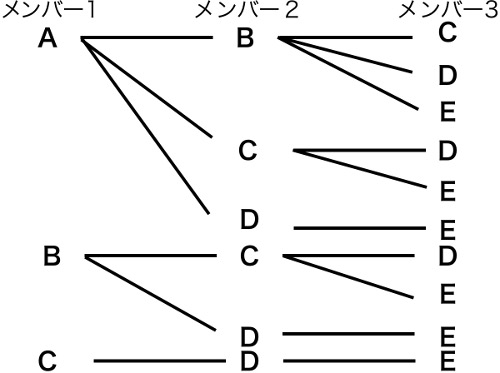
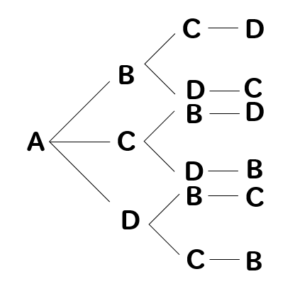
何通りあるか 計算 小学生- (3) a さんは選ばれ、c さんは選ばれない方法は何通りあるか。 この問題では、\(15\) 人から \(5\) 人を 選ぶだけ なので、選ぶ順番や並び順は考慮しません。 また問題によっては樹形図ではなく表や計算を使って考えた方が解きやすい問題もあります。 場合の数② 並べ方 例題1 a君、b君、c君、d君の4人でソフトボール投げをしました。投げる順番は何通りあるか求めなさい。 解説
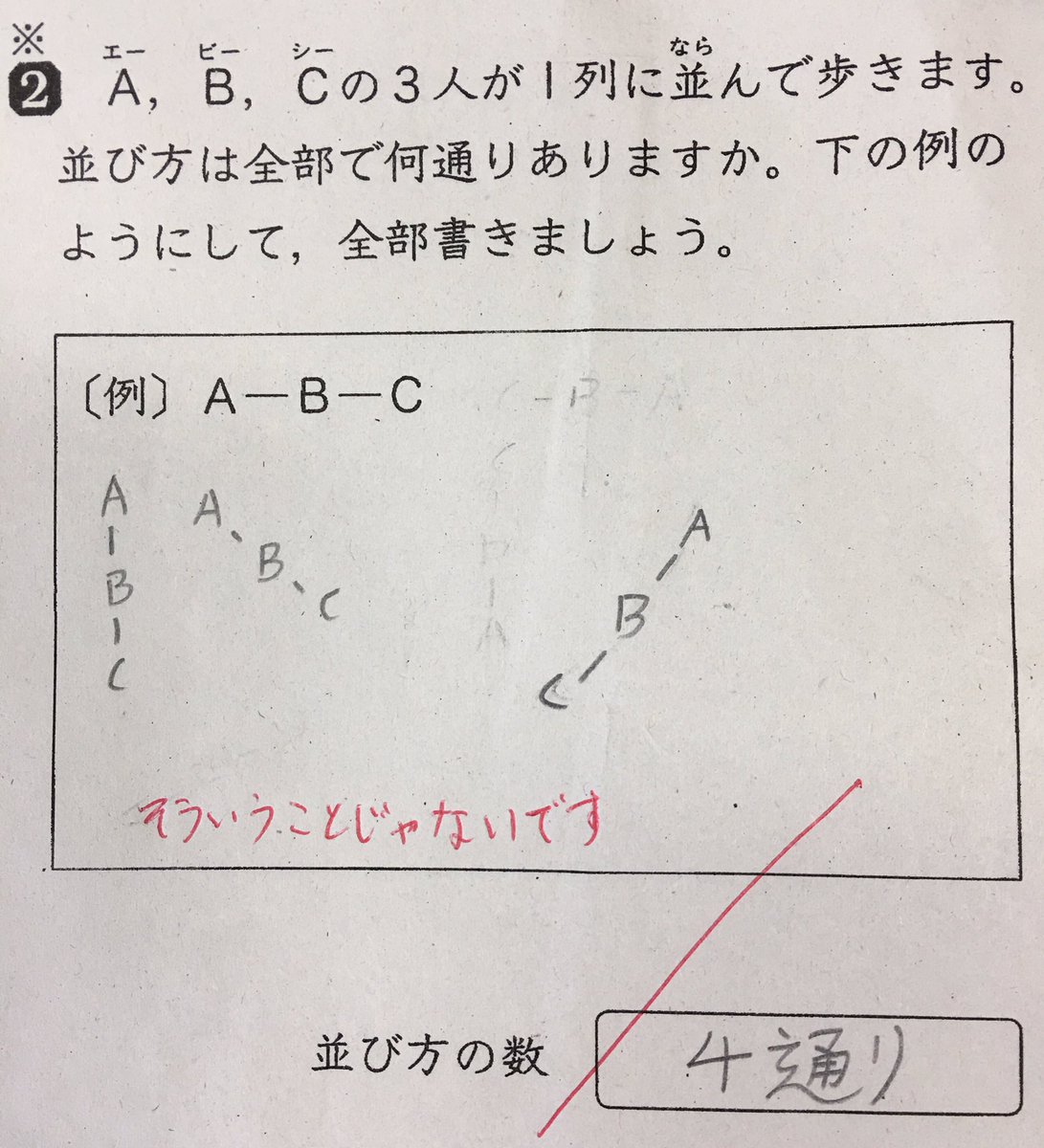
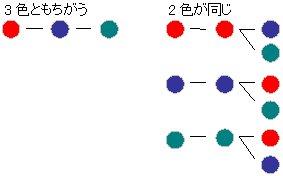
3人が1列に並ぶ並び方は何通り に対して小学生が出した答えが斜め上 話題の画像プラス
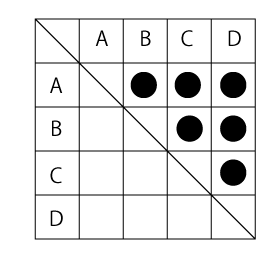
数学・算数 小学生の算数:何通りかの計算 大変お恥ずかしいのですが『何通りあるかの計算』について教えてください。 小学5・6年で習ったのですが、年近く経過して、すっかり忘れてしまいました。 質問No5人を2つのグループに分ける方法は何通りあるか。 はいはい重複順列の組分けパターンね、じゃあ計算はっと $2^52=2\cdot 2\cdot 2\cdot 2\cdot 22=30$通りカード$\fbox{A1}$と$\fbox{}$の並べ替えは$2!$通りあるので,カード$\fbox{A}$の区別をなくすことで同じ並びになるものは$5!$通りの中に$2!$通りずつあることになります. $の合計5枚のカードを一列に並べてできる並びは全部で何通りか. と計算でき,2つの
①まずは同じものも区別がつくとして、全部で何通りか計算する ②ダブっている数だけ割る。 同じものが2つなら 2×1=2 の2で割る。 同じものが3つなら 3×2×1=6 の6で割る。 ③同じものを含むカードが2種類ある場合は、②の割る計算を2回行う。それでは a, a, b, c というように同じ要素を含む場合で、この 4 文字を並べるとしたら、方法は何通りになるでしょうか。 もちろん答えは、\({}_4p_4=24\) 通りにはなりません。a が 2 つあるので、必ずこれよりも少なくなります。次のような枚数の硬貨があるとき,そのうちの一部または全部を用いてちょうど支払うことのできる金額は何通りあるか。 (1)100円硬貨4枚,50円硬貨1枚,10円硬貨3枚 これは簡単です! 「それぞれの硬貨を何枚使うことができるか」を考えていけばOKです
何通りあるか 計算 小学生のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
「何通りあるか 計算 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「何通りあるか 計算 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「何通りあるか 計算 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「何通りあるか 計算 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「何通りあるか 計算 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「何通りあるか 計算 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「何通りあるか 計算 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「何通りあるか 計算 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「何通りあるか 計算 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「何通りあるか 計算 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
「何通りあるか 計算 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |
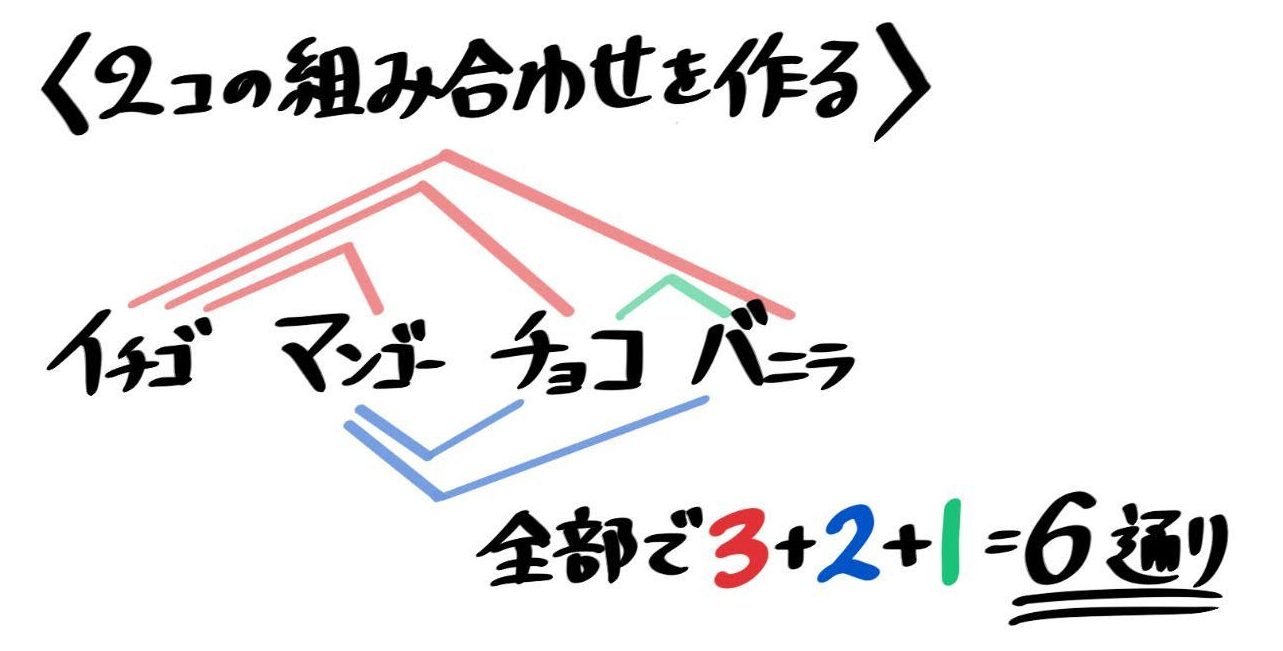
何通りの数ができますか。 高校生であれば余裕でできるというものでもないので、小学生に計算式主体で解かせるのかなりの上位層を除けば教える必要がないと思います。 私立中学の場合は学校による差も大きいですが、ある程度上の中学校だと計算 まずは、"順列"と"組み合わせ"の違いは何なのかをみていきましょう。 例えば、a,b,c,dという4つの文字があったとします。この中から2つの文字の並べ方(選び方)は何通り?とあったとします。 これは、『4 x 3=12通り』となります。
Incoming Term: 何通りあるか 計算 小学生,




0 件のコメント:
コメントを投稿